9. Diaprojector (In Dutch).

Voor De Museumfabriek te Enschede is er een workshop ontwikkeld waarbij een projector voor dia’s gemaakt kan worden. Hier worden experimenten beschreven die met deze dia projector kunnen worden uitgevoerd. We projecteren onder andere een dia met de tekst, de “Magie van licht” op een scherm. Verder onderzoeken we de afbeeldingswet van de geometrische optica en bepalen de brandpuntsafstand van de afbeeldingslens.

In de natuurkunde maken we gebruik van natuurkunde wetten om een “theorie” te maken waarmee we voorspellingen kunnen doen. De theorie wordt daarna met een experiment getoetst om te kijken of de wetten goed zijn. Dit heet “wetenschap”. Hier gaan we dus een wetenschappelijk onderzoek doen!

9.1. Twee optica wetten.

Om te voorspellen waar het scherm moet worden geplaatst om een scherp beeld te krijgen maken we gebruik van twee “optica wetten”:

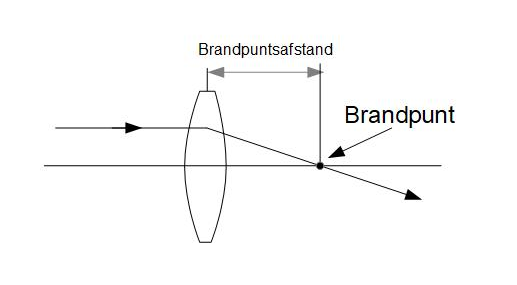
Wet 1: Een lichtstraal die loodrecht op een lens valt zal gebogen worden naar het brandpunt achter die lens.

Wet 2: Een lichtstraal die door het midden van een lens gaat wordt niet gebogen door de lens en gaat dus ongestoord verder.

Een lichtstraal, afkomstig van een willekeurig punt op het voorwerp, die loodrecht op de lens valt, zal zodanig gebroken worden dat hij door het brandpunt van de lens gaat. Het woord “brandpunt” zegt eigenlijk al genoeg. Zonnestralen vallen loodrecht op een lens omdat de zon heel ver weg staat en de lichtstralen vrijwel evenwijdig lopen. Daardoor gaan al de zonnestralen door het brandpunt van de lens. De lichtsterkte in dat punt wordt daardoor zo hoog dat je je lelijk kunt branden. Ook is het mogelijk om papier in brand te steken als je het in het brandpunt houdt. Probeer dat maar eens met een vergrootglas wat natuurlijk ook een lens is. Doe wel voorzichtig en kijk nooit met een lens of ieder ander optisch instrument (verrekijker) naar de zon! Je kunt daarmee gemakkelijk je oog beschadigen.

Een lichtstraal die door het midden van een lens gaat ziet eigenlijk twee evenwijdige glasvlakken zoals bij gewoon vensterglas. Net zoals dat bij vensters het geval is wordt de straal daarom niet gebroken.

9.2. Het maken van een afbeelding op een scherm.

We gaan nu de twee optica wetten gebruiken om te voorspellen waar de afbeelding van het voorwerp terechtkomt. In dat punt zetten we dan het scherm en kunnen we de afbeelding bekijken. Vanuit een willekeurig punt op het voorwerp vertrekken natuurlijk een heleboel stralen. Sommige daarvan zullen op de lens vallen. We bekijken nu twee speciale stralen die voldoen aan de twee optica-wetten: een loodrecht invallende straal en een straal die door het midden van de lens gaat.

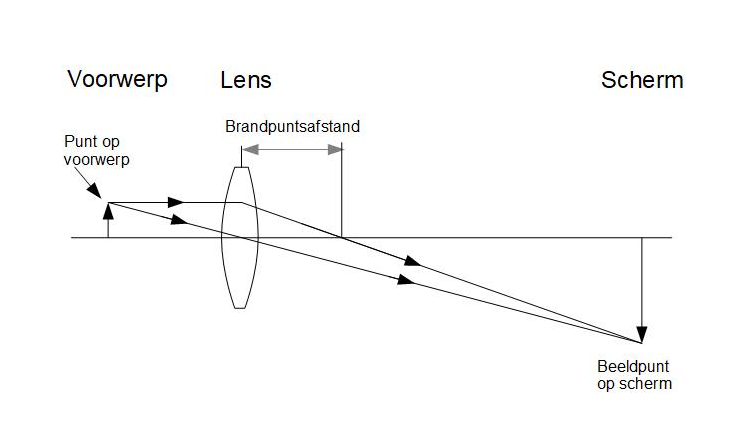
Toepassing van wet 1 en 2 om de plaats van het scherm te voorspellen.

Deze twee stralen gaan door de lens en kruisen elkaar in het beeldpunt. In dat punt zetten we het scherm. Nu is het zo dat ook alle andere stralen die uit het punt op het voorwerp vertrekken en door de lens gaan in hetzelfde beeldpunt terechtkomen! Omdat we het punt op het voorwerp willekeurig hebben gekozen zal elk punt op het voorwerp een overeenkomstig punt op het scherm hebben. Zo kunnen we dus het beeld beschouwen als een verzameling beeldpunten die afkomstig zijn van overeenkomstige punten op het lichtgevende voorwerp.

9.3. Uitvoering van het afbeeldingsexperiment (Niveau 1, basisonderwijs).

We gaan nu het afbeeldingsexperiment stap voor stap uitvoeren. Als voorwerp gebruiken we de dia met de afbeelding van een mm-verdeling. Behalve de positie van het scherm gaan we ook de vergroting meten en vergelijken met de theorie. Voor het maken van de tekening om de positie van het scherm te kunnen voorspellen hebben we de waarde van de brandpuntsafstand van de lens nodig. Die gaan we dus eerst meten.

9.4. Meting van de brandpuntsafstand van de lens.

1. Zet de lamp op het uiteinde van de rail en schakel hem aan.

2. Zet de diahouder vlak achter de lamp en plaats de dia met de mm-verdeling in de houder.

3. Plaats de lens ergens op de rail en plaats het spiegeltje achter de lens zodat het licht teruggekaatst wordt in de richting van de lamp.

4. Schuif met de lens (en de spiegel) zodanig dat je op het witte schermpje onder de mm-verdeling een scherp beeld ziet. Het beeld van de mm-verdeling staat op zijn kop.

5. Meet met een liniaal de afstand van de dia tot de lens. Deze afstand is gelijk aan de brandpuntsafstand van de lens.

9.5. Bepaling van de plaats van het scherm.

1. Leg een lang vel papier voor de rail. Het papier moet minstens 60 cm lang en 10 cm breed zijn. Plak hiertoe twee of drie vellen A4 (bijvoorbeeld printer papier) aan elkaar met plakband.

2. Trek een horizontale lijn van 60 cm of langer in het midden van het papier. Deze lijn stelt de “optische” as voor. De optische as is de lijn die de straal aangeeft die door het midden van alle optische componenten gaat, dus ook door het midden van de lens. Bovendien staat deze straal loodrecht op de lens. Hij gaat dus volgens de twee eerder genoemde wetten zowel door het brandpunt van de lens en wordt niet door de lens gebroken.

3. Zet de rail met daarop de lamp, de diahouder met daarin de dia met de mm-verdeling en de lens naast het papier.

4. Plaats de lens op een afstand van ongeveer 15 cm vanaf de dia.

5. Teken twee lijnen loodrecht op de optische as die de plaatsen van de dia en de lens aangeven.

6. Teken een punt op de lijn van de dia 1 cm boven de optische as.

7. Teken een punt op de optische as op een afstand gelijk aan de brandpuntsafstand achter de lens. Dit punt is het brandpunt van de lens.

8. Trek een horizontale lijn naar de lens op 1 cm hoogte boven de optische as. Omdat deze lijn (straal) loodrecht op de lens valt zal hij gebroken worden naar het brandpunt van de lens. Trek de lijn door zodanig dat hij door het brandpunt gaat. Probeer het tekenen van de lijn en punten zo nauwkeurig mogelijk te doen.

9. Trek een rechte lijn vanuit het punt op het voorwerp 1 cm boven de optische as door het midden van de lens. Volgens de tweede wet zal deze lijn (straal) ongebroken verder gaan. Trek hem door net zo ver als nodig is om de ander lijn te kruisen.

10. Teken een lijn loodrecht op de optische as die door het kruispunt gaat. Deze lijn geeft de plaats aan waar je het scherm moet zetten om een scherp beeld van de dia te krijgen.

11. Het beeld dat je ziet is een vergroting van de dia. Je kunt nu ook de vergroting meten en vergelijken met het resultaat van je tekening. Meet met een lineaal de afstand tussen twee lange streepjes op het beeld en vergelijk deze afstand met de afstand van het beeldpunt onder de optische as tot de optische as.

Je tekening (en meetopstelling) zou er nu ongeveer als volgt uit moeten zien:

Meetopstelling met tekening van de lichtstralen.

Is alles gelukt en kloppen de metingen met de voorspelling? Zo niet probeer het nogmaals en probeer zo nauwkeurig mogelijk te tekenen. Probeer hetzelfde te doen voor andere posities van de lens op de rail. Als je al goed in wiskunde bent zou je ook de metingen kunnen uitvoeren voor niveau 2. Voor de metingen bij niveau 2 maken we gebruik van wiskundige formules voor de afbeeldingswetten en zetten we de meetresultaten uit in grafieken, zodanig dat er rechte lijnen in de grafiek verschijnen. Je kunt dan veel nauwkeuriger meten en bovendien in één oogopslag zien of de metingen overeenkomen met de theorie en of je alle meetpunten goed gemeten hebt. Niveau 2 is bedoeld voor leerlingen van het voortgezet onderwijs.

9.6. Uitvoering van het afbeeldingsexperiment (Niveau 2, voortgezet onderwijs, HBO, 1e jaars universiteit).

We gaan nu het afbeeldingsexperiment opnieuw uitvoeren maar nu met behulp van de afbeeldingsformules:

\(\frac{1}{ v } + \frac{1}{b} = \frac{1}{f}\) (1)

\(V=-\frac{b}{v}\) (2)

Hierin zijn:

v: voorwerpsafstand = afstand voorwerp (dia) tot de lens.

b: Beeldafstand = afstand lens tot het beeld (scherm)

f: brandpuntsafstand van de lens

V: vergroting = afmeting van het beeld gedeeld door de afmeting van het voorwerp

Het min-teken in formule (2) is daar omdat het beeld op zijn kop staat. We kunnen formule (1) ook schrijven als: \(\frac{1}{b}=-\frac{1}{v}+\frac{1}{f}\). We zien hieruit dat deze formule van de vorm \(y=ax+b\) is. Dus een rechte lijn met richtingscoëfficiënt, \(a=-1\), en afsnede met de y-as, \(b=\frac{1}{f}\). We gaan daarom de meetresultaten zodanig in een grafiek tekenen dat er een rechte lijn ontstaat. We kunnen dan in één oogopslag zien of de afbeeldingswet geldig is en of we alle meetpunten correct gemeten hebben.

Iets dergelijks gaan we ook doen voor de vergroting, V . Uit formule (1) volgt: \(b=\frac{fv}{v-f}\), zodat we met formule (2) vinden: \(V=-\frac{f}{v-f}\). Ook nu kunnen we een rechte lijn in een grafiek krijgen als we \(\frac{1}{V}\) uitzetten tegen v. Immers \(\frac{1}{V}=-\frac{1}{f}v+1\).

9.7. Stap voor stap uitvoering van het experiment.

1. Maak een tabel met de kolommen v[m], b[m], 1/v[1/m], 1/b[1/m], V[-] en 1/V[-].

2. Zet de lamp en daar vlak achter de diahouder met de mm verdeling op de rail en schakel de lamp aan.

3. Zet de lens op 12 cm afstand van de dia.

4. Zet het scherm op zodanige afstand dat er een scherp beeld ontstaat.

5. Meet de afstand van de lens tot het scherm en de afstand tussen twee lange streepjes van het beeld. Dit is gelijk aan de vergroting omdat de afstand tussen de overeenkomstige streepjes van het voorwerp precies 1 cm is. Natuurlijk moet je in dit geval de grootte van het beeld daarom ook in cm’s uitdrukken!

6. Herhaal de bovenstaande meting voor v = 13 cm, 14 cm , … tot en met 22 cm.

7. Converteer cm’s naar m’s, bereken 1/v, 1/b en 1/V en zet alles in de tabel.

8. De tabel ziet er nu als volgt uit. Maak hem verder af met jouw meetresultaten. NB de metingen gegeven in de eerste rij kunnen afwijken van jouw waarden. Ze dienen ter illustratie, vervang ze zo nodig:

v[m]	b[m]	1/v[1/m]	1/b[1/m]	V[-]	1/V[-]
0.12	0.825	8.33	1.21	6.6	0.15
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.20
0.21
0.22

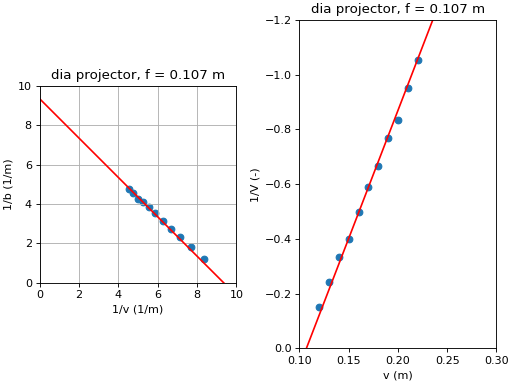
We drukken de meetwaarden uit in meters omdat er op die manier ‘mooie getallen’ op de assen van de grafiek komen te staan. Maak een grafiek met gelijke horizontale en verticale assen van 0 tot 10. Maak ook een grafiek waarin je de inverse van de vergroting uitzet tegen de voorwerpafstand. Als je alles correct hebt uitgevoerd moeten deze grafieken er ongeveer als volgt uitzien:

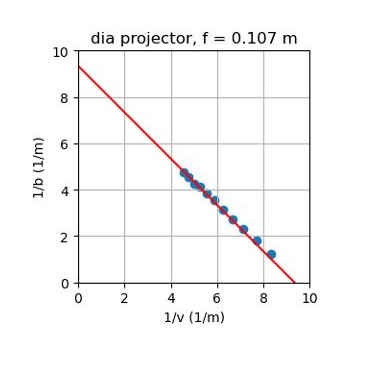
Inverse van de beeldafstand als functie van de inverse voorwerpafstand. De rode lijn is volgens de theorie met de gemeten brandpuntsafstand.

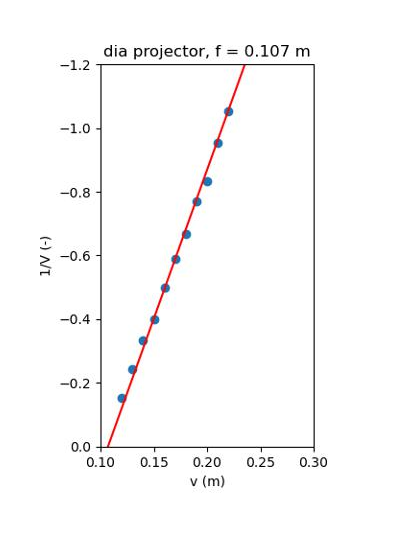
Inverse vergroting als functie van de voorwerpafstand. De rode lijn is volgens de theorie met de gemeten brandpuntsafstand.

9.8. Meetfouten.

In de bovenstaande tabel staan de gemeten waarden voor de voorwerpafstand, v, de beeldafstand, b, en de vergroting, V. Let op dat er geen kolommen met de waardes van de meetfouten zijn. Dat zou eigenlijk wel moeten, elke meting in de natuurkunde hoort vergezeld te zijn van een opgave van de fout in de meting. Deze meetfouten werken door in het resultaat van het experiment. Dat hoort bij een hoger niveau 3: Hogeschool en Universiteit.

9.9. Appendix 1.

Een Python programma kun je eventueel gebruiken voor het presenteren van de meetresultaten.

(Source code, png, hires.png, pdf)

Echter, met pen, papier en een lineaal kom je ook heel ver…