7.3.1. Generation of a 2-dimensional Airy beam from a Gaussian laser beam.

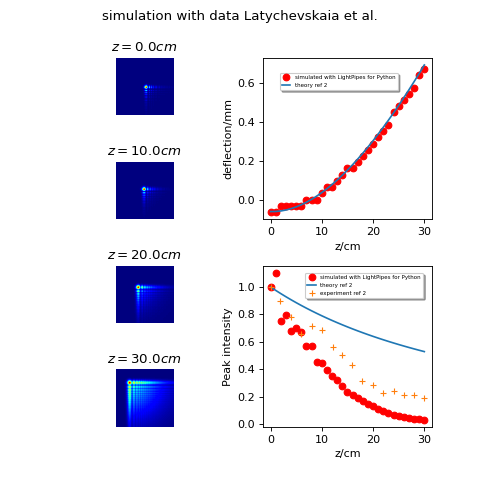
A two-dimensional Airy beam can be generated by substituting a cubic phase distribution in a Gaussian beam followed by a Fourier transform by a positive lens. In the simulation below we repeat the simulations published by Latychevskaia et al. 1 and we compare the LightPipes simulation with their results.

References:

1

20. Latychevskaia, D. Schachtler, and H.W. Fink, “Creating Airy beams employing a transmissive spatial light modulator”, Appl. Opt. 55, 6095-6101 (2016).

(Source code)

(png, hires.png, pdf)

(png, hires.png, pdf)

7.3.2. Self-healing Airy beam.

In the video below we demonstrate the self-healing feature of Airy beams. A 2 mm diameter disk is placed in the path of the main lobe at z = 40 cm. After disturbing the beam, the beam’s shape recovers.

Playback Rate 1

The video was made with the following python script:

"""
Self healing Airy beam. A disk is placed at some distance from the origin.
This obstacle disturbs the beam, but it heals itself.
"""
from LightPipes import *
import matplotlib.pyplot as plt
import matplotlib.animation as animation

wavelength = 2.3*um
size = 30*mm
N = 500
x0=y0=1*mm
a1=a2=0.1/mm
w=1*mm
z= 0 *cm
dz = 2 *cm
fig, ax = plt.subplots(); ax.axis('off')
ims =[]

F0=Begin(size,wavelength,N)
F0=AiryBeam2D(F0,x0=x0, y0=y0, a1=a1, a2=a2)

for i in range(1000):
    if i == 20: # at z = 40 cm an obstacle is placed
        F0=CircScreen(F0,w)
    F=Fresnel(F0,z)
    I=Intensity(F)
    im = ax.imshow(I, animated = True, cmap='jet')
    s = r'$z = {:4.0f}$ cm'.format(z/cm)
    t = ax.annotate(s,(100,100), color = 'w') # add text
    ims.append([im,t])
    z += dz

ani = animation.ArtistAnimation(fig, ims, interval=5, blit=True,
                                repeat_delay=1000)
ani.save("movie.mp4")
plt.show()