7.8.3. Propagation in a lens-like, absorptive medium.

In this example we model the propagation of a Gaussian beam in a lens-like waveguide. The profile of the refractive index is chosen such, that the beam preserves approximately its diameter in the waveguide (we use the fundamental mode). We’ll consider the propagation of an axial mode, tilted with respect to the waveguide axis and a non-axial mode.

we use the approximation for the profile of the refractive coefficient, \(n'=n-i\kappa\) in the form: \(n(r)^2=n_0^2-n_0n_1r^2\). It is a well-known fact [1] that the half-width of the fundamental Gaussian mode of a lens-like waveguide is defined as: \(w_0^2=\frac{2}{k(n_0n_1)^{1/2}}\) , with \(k=\frac{2 \pi}{\lambda}\). For a waveguide of \(1 \times 1 mm, n_0=1.5, n_1=400 m^{-2}, \kappa = 1.0\) and \(\lambda = 1 \mu m\), the Gaussian mode has a diameter of \(226 \mu m\) . A tilt in the x-direction causes reflections in the waveguide as demonstrated in the next example of the propagation of a tilted Gaussian beam through the waveguide.

(Source code, png, hires.png, pdf)

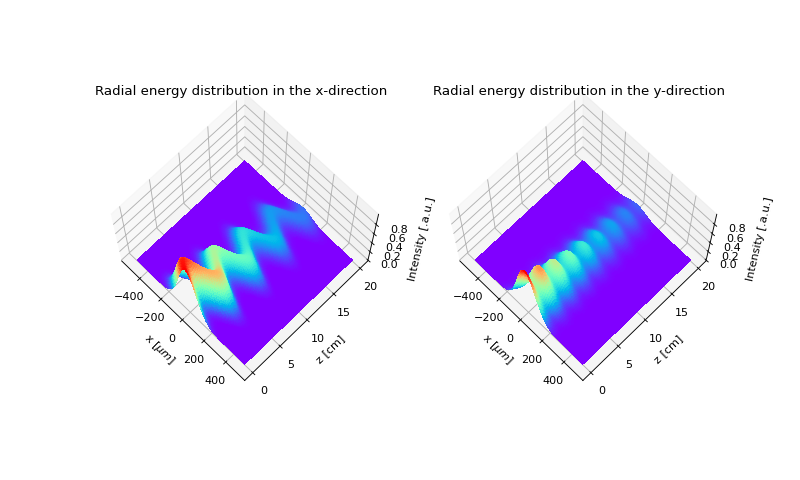
_images/LensLikeMedium.png

Propagation of a tilted Gaussian beam in a lens-like, absorptive medium.