8.3.5. Fabry Perot interferometer.
Download Python script: FabryPerot.py

Maurice Paul Auguste Charles Fabry (1867, Marseille – 1945)

Jean-Baptiste Alfred Perot (1863, Metz – 1925)
When two partial reflecting mirrors with reflectivity, \(R\), (transmission \(= 1 - R\)) are precisely aligned parallel, illuminated by a diffuse, broad, monochromatic source and are separated a distance, \(d\), from each other, a set of concentric rings can be observed on a screen after imaging with a lens. These rings are the result of interference of multiple beams and because of that, the Fabry Perot belongs to the class of multiple beam interferometers.The sharpness of the rings depends on the reflectivity of the mirrors and the ring- or fringe contrast is represented by the finesse of the Fabry Perot.
The Fabry Perot is very suitable to measure the wavelength difference of two sources emitting at wavelengths close together. In general the two wavelengths will produce two sets of concentric rings, which will overlap for certain conditions.
In the first experiment the 550 nm line (from a green mercury lamp) is splitted by some means (for example by the Zeeman effect) and is measured by variation of the distance, \(d\), between the mirrors.
In the second experiment a medium with refractive index larger than one is inserted between the mirrors and the index is measured, again by varying the distance between the two mirrors.

|

|
Experimental set-up of a Fabry Perot interferometer illuminated by a sodium (Na) lamp. The two Na D1 and D2 lines at 589.6 nm and 589.0 nm produce two sets of concentric rings observed with a CCD camera.
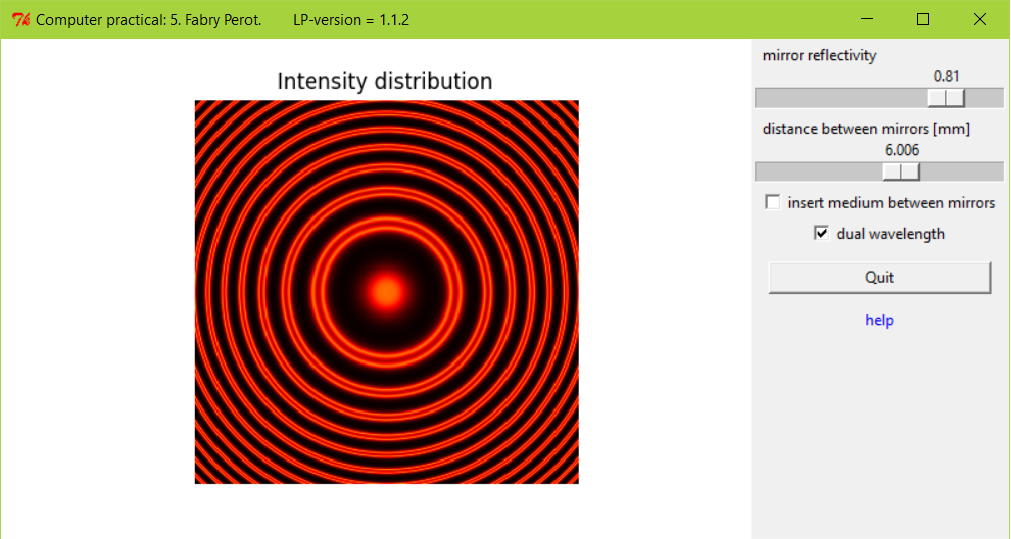
Screenshot of the Fabry Perot program.
Download Python script: FabryPerot.py
8.3.5.1. Measurement of the distance between two wavelengths.

Fabry Perot setup.
Show that, in air, overlap of the two sets of rings occurs for distances between the two mirrors: \(d_n=\frac{\lambda^2}{2\Delta\lambda}n\) where \(n\) is an integer. Note that the angles with the optical axis of all the rays forming the rings are very small. The wavelength separation, \(\Delta\lambda\), is very small compared to the average wavelength, \(\lambda\).
Choose a suitable value for the finesse of the Fabry Perot.
Switch on the line-splitting and measure the distances, \(d\), where overlap of the fringes occurs.
Calculate the wavelength-difference, \(\Delta\lambda\), from the measurements. The average (vacuum) wavelength, \(\lambda\), of the source is 550 nm.
8.3.5.2. Measurement of the refractive index of a medium.
Derive a theory from which the refractive index of a medium between the two mirrors can be determined from overlap-measurements (modify the formula derived for experiment 5.1)
Switch on the line-splitting and the medium and measure the distances, \(d\), where overlap of the fringes occurs.
Determine the refractive index, \(n_f\), from the measurements using the wavelength measured in the first experiment.
8.3.5.3. Questions about the Fabry Perot interferometer.
Calculate the finesse of this Fabry Perot for mirror reflectivity \(R\) = 70%.
What is the minimum wavelength separation that can be measured for a distance between the mirrors of 2.0 mm and at reflections of 70 %?
Can one measure the separation of the two yellow sodium D-lines with the overlap method of the Fabry Perot set-up of this exercise?