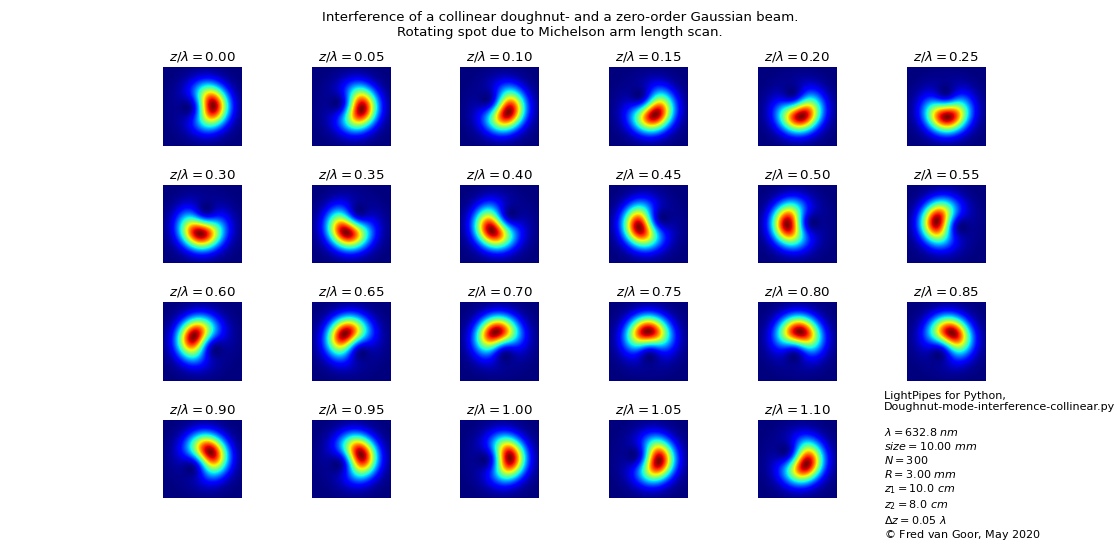
7.1.4. Interference of a doughnut laser beam: collinear beams.

When a doughnut beam interferes with a fundamental Gauss beam the resulting interference pattern shows a lobe which rotates depending on the difference in path between the two beams. Of course both beams must originate from the same laser source to have the same initial phase. The doughnut beam can be made by inserting a spiral phase plate in one of the two beams. When the two beams interfere and when they are collinear, the interference pattern shows a rotating lobe when the path difference between the two beams is varied:

#! /usr/bin/env python
"""
    Doughnut_collinear.py

    Interference of a collinear zero order beam with a  Laguerre-Gauss
    doughnut beam.
    The interferometer could be a Michelson instrument.

    cc Fred van Goor, May 2020.
"""
from LightPipes import *
import matplotlib.pyplot as plt

if LPversion < "2.0.0":
    print(r'You need to upgrade LightPipes to run this script.' + '\n'+r'Type at a terminal prompt: $ pip install --upgrade LightPipes')
    exit(1)

wavelength=632.8*nm #wavelength of HeNe laser
size=10*mm # size of the grid
N=300 # number (NxN) of grid pixels
R=3*mm # laser beam radius

z1=10*cm # length of path 1
z2=8*cm # length of path 2
dz=0.05*wavelength #step of path 2

#initiate plots:
fig, _axs = plt.subplots(nrows=4, ncols=6,figsize=(14.0,7.0))

s=r'Interference of a collinear doughnut- and a zero-order Gaussian beam.' +'\n'\
r'Rotating spot due to Michelson arm length scan.'
fig.suptitle(s)
fig.subplots_adjust(hspace=0.5)
axs = _axs.flatten()

F=Begin(size,wavelength,N)
F1=GaussBeam(F,R,doughnut=True,n=0,m=1) #beam 1: doughnut  Laguerre-Gauss
F1=Forvard(z1,F1) #propagate path 1

F2=GaussBeam(F,R) #beam 2: TEM00 Gauss
F2=Forvard(z2,F2) #propagate path 2

for i in range(23):
    F2=Forvard(dz,F2) #step path 2
    F=BeamMix(F1,F2) #add the two beams
    I=Intensity(0,F) #intensity at the observing screen
    #make the plots:
    s=r'$z/\lambda = $' + r'{:4.2f}'.format(i*dz/wavelength)
    axs[i].imshow(I,cmap='jet'); axs[i].axis('off'); axs[i].set_title(s)

s = r'LightPipes for Python,' + '\n' + 'Doughnut-mode-interference-collinear.py'+ '\n\n'\
    r'$\lambda = {:4.1f}$'.format(wavelength/nm) + r' $nm$' + '\n'\
    r'$size = {:4.2f}$'.format(size/mm) + r' $mm$' + '\n'\
    r'$N = {:4d}$'.format(N) + '\n'\
    r'$R = {:4.2f}$'.format(R/mm) + r' $mm$'+ '\n'\
    r'$z_1 = {:4.1f}$'.format(z1/cm) + r' $cm$' + '\n'\
    r'$z_2 = {:4.1f}$'.format(z2/cm) + r' $cm$' + '\n'\
    r'$\Delta{z} = ' + '{:4.2f}$'.format(dz/wavelength) + r' $\lambda$' + '\n'\
    r'${\copyright}$ Fred van Goor, May 2020'

axs[23].text(0,-0.5,s)
axs[23].axis('off')

plt.show() #show the results

(Source code, png, hires.png, pdf)