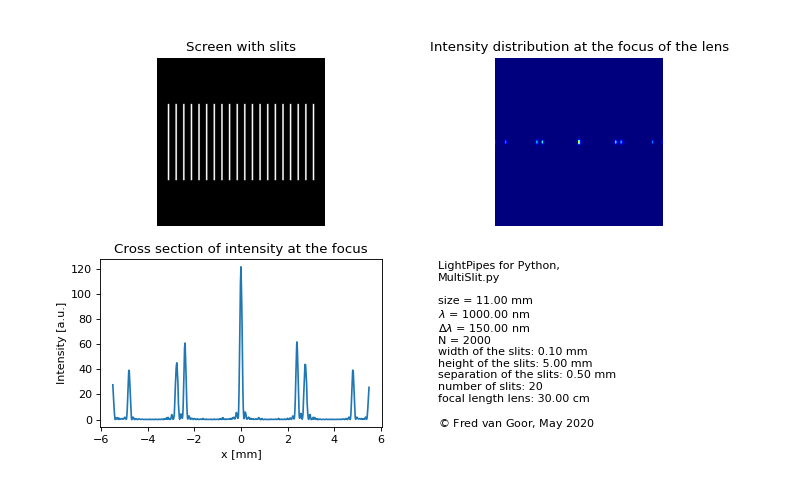
7.1.3. Multi- holes and slits.
In this example we demonstrate the use of a number of holes or slits in a row. In this way it is possible to make a grating. There are two wavelengths in the beam which demonstrates the use of a grating as a spectrometer. The intensities of the two fields can be simply added after separate propagations.
#! python3
import numpy as np
import matplotlib.pyplot as plt
from LightPipes import *
"""
MultiSlit.py
Demonstrates the RowOfFields command. Two wavelengths are used to show
the principles of a grating.
cc Fred van Goor, June 2020.
"""
wavelength=1000*nm
Dlambda=150*nm
size=11*mm
N=2000
N2=int(N/2)
SlitSeparation=0.5*mm
f=30*cm
Nslits=20
SlitHeight=5*mm
SlitWidth=0.1*mm
Nheight=int(SlitHeight/size*N)
Nwidth=int(SlitWidth/size*N)
Fslit=np.ones((Nheight,Nwidth))
F1=Begin(size,wavelength,N)
F1=RowOfFields(F1,Fslit,Nslits,SlitSeparation)
Islits=Intensity(F1)
F1=Lens(F1,f)
F1=Forvard(F1,f)
F11=Interpol(F1,size,N,magnif=4)
Iscreen1=Intensity(F11)
F2=Begin(size,wavelength+Dlambda,N)
F2=RowOfFields(F2,Fslit,Nslits,SlitSeparation)
F2=Lens(F2,f)
F2=Forvard(F2,f)
F22=Interpol(F2,size,N,magnif=4)
Iscreen2=Intensity(F22)
F3=BeamMix(F11,F22)
Iscreen3=Intensity(F3)
print(F22.lam/nm)
X=np.arange(N)
X=(X/N-1/2)*size/mm
s= r'LightPipes for Python,' + '\n' +\
r'MultiSlit.py'+ '\n\n'\
r'size = {:4.2f} mm'.format(size/mm) + '\n' +\
r'$\lambda$ = {:4.2f} nm'.format(wavelength/nm) + '\n' +\
r'$\Delta\lambda$ = {:4.2f} nm'.format(Dlambda/nm) + '\n' +\
r'N = {:d}'.format(N) + '\n' +\
r'width of the slits: {:4.2f} mm'.format(SlitWidth/mm) + '\n' +\
r'height of the slits: {:4.2f} mm'.format(SlitHeight/mm) + '\n' +\
r'separation of the slits: {:4.2f} mm'.format(SlitSeparation/mm) + '\n' +\
r'number of slits: {:d}'.format(Nslits) + '\n' +\
r'focal length lens: {:4.2f} cm'.format(f/cm) + '\n\n' +\
r'${\copyright}$ Fred van Goor, May 2020'
fig=plt.figure(figsize=(10,6))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222);#ax2.set_ylim(bottom=900,top=1100)
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224)
ax1.imshow(Islits,cmap='gray',aspect='equal');ax1.axis('off'); ax1.set_title('Screen with slits')
ax2.imshow(Iscreen1+Iscreen2,cmap='jet',aspect='equal');ax2.axis('off'); ax2.set_title('Intensity distribution at the focus of the lens')
#ax2.margins(x=0, y=-0.45)
ax3.plot(X,(Iscreen1+Iscreen2)[N2]); ax3.set_xlabel('x [mm]'); ax3.set_ylabel('Intensity [a.u.]'); ax3.set_title('Cross section of intensity at the focus')
ax4.text(0,0,s); ax4.axis('off')
plt.show()
(Source code, png, hires.png, pdf)
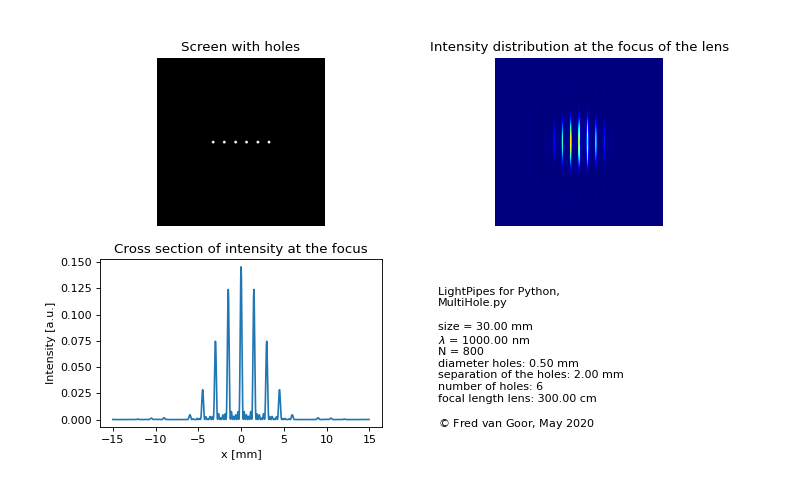
Below we demonstrate interference from a row of holes.
#! python3
import numpy as np
import matplotlib.pyplot as plt
from LightPipes import *
"""
MultiHole.py
Demonstrates the MultiHole command. Two wavelengths are used to show
the principles of a grating.
cc Fred van Goor, June 2020.
"""
wavelength=1000*nm
size=30*mm
N=800
N2=int(N/2)
HoleSeparation=2*mm
z=300*cm
Nholes=6
size_hole=1*mm
HoleDiameter=0.5*mm
Ndiameter=int(HoleDiameter/size*N)
Nhole=int(size_hole/size*N)
Fhole=Begin(size_hole,wavelength,Nhole)
Fhole=CircAperture(Fhole,HoleDiameter/2)
F=Begin(size,wavelength,N)
F=RowOfFields(F,Fhole,Nholes,HoleSeparation)
Iholes=Intensity(F)
X=np.arange(N)
X=(X/N-1/2)*size/mm
F=Lens(F,z)
F=Fresnel(F,z)
Iscreen=Intensity(F)
s= r'LightPipes for Python,' + '\n' +\
r'MultiHole.py'+ '\n\n'\
r'size = {:4.2f} mm'.format(size/mm) + '\n' +\
r'$\lambda$ = {:4.2f} nm'.format(wavelength/nm) + '\n' +\
r'N = {:d}'.format(N) + '\n' +\
r'diameter holes: {:4.2f} mm'.format(HoleDiameter/mm) + '\n' +\
r'separation of the holes: {:4.2f} mm'.format(HoleSeparation/mm) + '\n' +\
r'number of holes: {:d}'.format(Nholes) + '\n' +\
r'focal length lens: {:4.2f} cm'.format(z/cm) + '\n\n' +\
r'${\copyright}$ Fred van Goor, May 2020'
fig=plt.figure(figsize=(10,6))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222);# ax2.set_ylim(bottom=130,top=170)
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224)
ax1.imshow(Iholes,cmap='gray',aspect='equal');ax1.axis('off'); ax1.set_title('Screen with holes')
ax2.imshow(Iscreen,cmap='jet',aspect='equal');ax2.axis('off'); ax2.set_title('Intensity distribution at the focus of the lens')
ax3.plot(X,Iscreen[N2]); ax3.set_xlabel('x [mm]'); ax3.set_ylabel('Intensity [a.u.]'); ax3.set_title('Cross section of intensity at the focus')
ax4.text(0,0,s); ax4.axis('off')
plt.show()
(Source code, png, hires.png, pdf)